[OpenMP] Exercise 2 : Compute PI

This material is part of the course Practical Introduction to Parallel Programming and meant for educational purposes only.

Background

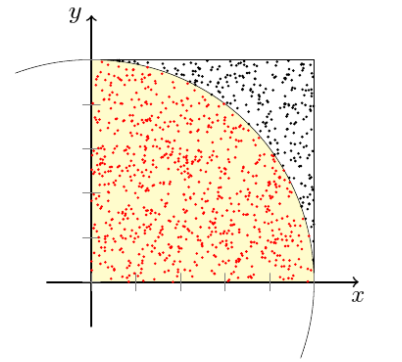
The area of a circle of radius \(R\) is \(\pi R^2\), the area of a square with side length \(2R\) is \(4R^2\). If the circle is inscribed inside the square then the ratio of both areas is \(\pi/4\).

Monte Carlo method

If we pick \(N\) points at random inside the square and count the number of points that are inside the circle (\(M\)) then we can compute the approximation \(\pi\approx 4M/N\).

Hints

You can retrieve an upper bound of the numbers of threads that will be created in a parallel regions using omp_get_max_threads(). This even works outside any parallel region.

Use an array of size omp_get_max_threads() to pass data from the different threads to the master thread.

Use #pragma omp parallel default(none) to force yourself to specify the behaviour of all variables (private/shared) explicitly.

Cole este comando no seu terminal:

A senha para conectar é

Questão 1: Compute PI

#include <stdio.h>
#include <stdarg.h>
#include <stdlib.h>
#include <string.h>

#ifdef _OPENMP
#include "omp.h"
#else
#define omp_get_num_threads() 1
#define omp_get_max_threads() 1
#define omp_get_thread_num()  0
#endif

/* ---------------------------------------------------------------------
 * global variables, constants and types
 * ------------------------------------------------------------------ */

struct                      conf
{
  int                       steps;
};

typedef struct conf       conf_t;

/* ---------------------------------------------------------------------
 * error()
 * ------------------------------------------------------------------ */

void                      error

  ( const char*             fmt, ... )

{
  va_list  ap;

  va_start  ( ap, fmt );
  fprintf   ( stderr, "\n*** ERROR: " );
  vfprintf  ( stderr, fmt, ap );
  fprintf   ( stderr, "\n\n" );
  va_end    ( ap );
  exit      ( 1 );
}

/* ---------------------------------------------------------------------
 * parse_args()
 * ------------------------------------------------------------------ */

void parse_args

  ( conf_t*                 conf,
    int                     argc,
    char**                  argv )

{
    const int  root = 0;

    int        iarg;

    /* Set default values. */

    conf->steps  = 1000;

    for ( iarg = 1; iarg < argc; iarg++ )
    {
        if ( strcmp( argv[iarg], "--steps" ) == 0 )
        {
            iarg++;

            if ( iarg >= argc )
            {
                error ( "no number of steps specified" );
            }

            if ( sscanf( argv[iarg], " %d", &conf->steps ) != 1 ||
                 (conf->steps < 0) )
            {
                error ( "invalid number of steps specified" );
            }

            continue;
        }
    }
}

/* ---------------------------------------------------------------------
 * main()
 * ------------------------------------------------------------------ */

int                       main

  ( int                     argc,
    char**                  argv )

{
    conf_t       conf;
    int          i;
    int          M=0;
    int          nproc;
    unsigned int seed=0;

    parse_args ( &conf,  argc,  argv );

    /* Monte Carlo calculation of PI */
    for (i=0; i<conf.steps; i++)
        {
            double x = rand_r(&seed)/(double)RAND_MAX;
            double y = rand_r(&seed)/(double)RAND_MAX;

            if (x*x + y*y < 1.0)
                M++;
        }

    /* Output */
    printf("Approximation of PI = %g\n", 4*M/(double)conf.steps);

    return 0;
}

Questão 2: OpenMP environment variables

Specify the OpenMP environment variables that should be used for running your program (export OMP_NUM_THREADS=1 ...). Use semicolons to separate multiple variables

Questão 3: Command Line Argument

Specify the command line arguments that should be passed to your program when it is run. Arguments must be given in quotes and separated by commas. Leave this filed empty if you do not want to specify command line arguments.

Example: "1","int","arg=2" is interpreted as three arguments 1, int, and arg=2.

Autores	Erik-Jan Lingen, Matthias Möller
Prazo de entrega	Sem prazo
Limite de submissão	No limitation

Informações

Entrar